Aplikasi
Matriks
dalam Kriptografi Hill Cipher
by Maya Gishella (120170026)
Hill
Cipher merupakan salah satu algoritma kriptografi kunci simetris. Algoritma
Hill Cipher menggunakan matriks berukuran m x m sebagai kunci untuk melakukan
enkripsi dan dekripsi. Dasar teori matriks yang digunakan dalam Hill Cipher
antara lain adalah perkalian antar matriks dan melakukan invers pada matriks.
Matriks
adalah susunan sklar elemen- elemen dalam bentuk baris dan kolom [4]. matriks A
yang berukuran dari m baris dan n kolom (m x n) adalah : Entri aij disebut elemen
matriks pada baris ke-i dan
kolom
ke-j. Jika m = n, maka matriks tersebut dinamakan juga matriks bujursangkar
(square matrix). Matriks yang elemen aij dimana i = j = 1 dan elemen yang lain
adalah 0 disebut matriks identitas (I). Sebuah matriks B disebut invers dari
matriks A jika AB = I. B biasa ditulis A-1.
Operasi
Aritmatika pada Matriks
Operasi
aritmetika yang biasa dilakukan terhadap matriks adalah operasi penjumlahan dan
perkalian dua buah matriks, serta perkalian matriks dengan sebuah skalar.
Penjumlahan dua buah matriks; dua buah matriks dapat dijumlahkan jika ukuran
keduanya sama. Penjumlahan dilakukan dengan menambahkan setiap elemen matriks
yang memiliki posisi sama.
Perkalian
dua buah matriks; Dua buah matriks dapat dikalikan jika jumlah kolom matriks
pertama sama dengan jumlah baris matriks kedua. Perkalian matriks A dan B yang
akan menghasilkan C dapat dituliskan sebagai
Perkalian
dengan matriks skalar; Misalkan k adalah sebuah skalar, maka perkalian matriks
A dengan skalar k adalah mengalikan setiap elemen matriks dengan k.
KRIPTOGRAFI
Kriptografi
berasal dari Bahasa Yunani: “cryptós” artinya rahasia, sedangkan “gráphein”
artinya tulisan. Jadi, secara morfologi kriptografi berarti tulisan rahasia.
Prinsip
Kerja Kriptografi
Pembakuan
penulisan pada kriptografi dapat ditulis dalam bahasa matematika. Fungsi-fungsi
yang mendasar dalam kriptografi adalah enkripsi dan dekripsi. Enkripsi adalah
proses mengubah suatu pesan asli (plaintext) menjadi suatu pesan dalam bahasa
sandi (ciphertext).
C = E (M)
dimana
:
M
= pesan asli
E
= proses enkripsi
C = pesan
dalam bahasa sandi
Sedangkan
dekripsi adalah proses mengubah pesan dalam suatu bahasa sandi menjadi pesan
asli kembali.
M = D (C)
D
= proses dekripsi
Umumnya,
selain menggunakan fungsi tertentu dalam melakukan enkripsi dan dekripsi,
seringkali fungsi itu diberi parameter tambahan yang disebut dengan istilah
kunci.
Jenis-jenis
Serangan
Selain
ada pihak yang ingin menjaga agar pesan tetap aman, ada juga pihak-pihak yang
ingin mengetahui pesan rahasia tersebut secara tidak sah. Bahkan ada
pihak-pihak yang ingin agar dapat mengubah isi pesan tersebut. Ilmu untuk
mendapatkan pesan yang asli dari pesan yang telah disandikan tanpa memiliki
kunci untuk membuka pesan rahasia tersebut disebut kriptanalisis. Sedangkan
usaha untuk membongkar suatu pesan sandi tanpa mendapatkan kunci dengan cara
yang sah dikenal dengan istilah serangan (attack). Di bawah ini dijelaskan
beberapa macam penyerangan terhadap pesan yang sudah dienkripsi:
1.
Ciphertext only attack, penyerang hanya mendapatkan pesan yang sudah
tersandikan saja.
a.
Known plaintext attack, dimana penyerang selain mendapatkan sandi, juga
mendapatkan pesan asli. Terkadang disebut pula clear-text attack.
b. Choosen
plaintext attack, sama dengan known
plaintext attack, namun penyerang bahkan dapat memilih penggalan mana
dari pesan asli yang akan disandikan.
Jenis-jenis
Kunci
Jenis
kunci dalam kriptografi terbagi menjadi 2, yaitu kunci simetris dan kunci
asimetris.
1)
Kunci Simetris
Ini
adalah jenis kriptografi yang paling umum dipergunakan. Kunci untuk membuat
pesan yang disandikan sama dengan kunci untuk membuka pesan yang disandikan
itu. Jadi pembuat pesan dan penerimanya harus memiliki kunci yang sama persis.
Siapapun yang memiliki kunci tersebut, termasuk pihak-pihak yang tidak
diinginkan, dapat membuat dan membongkar rahasia ciphertext. Problem yang
paling jelas disini terkadang bukanlah masalah pengiriman ciphertext- nya,
melainkan masalah bagaimana menyampaikan kunci simetris tersebut kepada pihak
yang diinginkan.
2)
Kunci Asimetris
Pada
pertengahan tahun 70-an Whitfield Diffie dan Martin Hellman menemukan teknik
enkripsi asimetris yang merevolusi dunia kriptografi. Kunci asimetris adalah
pasangan kunci-kunci kriptografi yang salah satunya dipergunakan untuk proses
enkripsi dan yang satu lagi untuk dekripsi. Semua orang yang mendapatkan kunci
publik dapat menggunakannya untuk mengenkripsikan suatu pesan, sedangkan hanya
satu orang saja yang memiliki rahasia tertentu, dalam hal ini kunci privat,
untuk melakukan pembongkaran terhadap sandi yang dikirim untuknya. Dengan cara
seperti ini, jika seorang pihak pertama mengirim pesan untuk pihak kedua, pihak
pertama tersebut dapat merasa yakin bahwa pesan tersebut hanya dapat dibaca
oleh pihak yang bersangkutan, karena hanya dia yang bisa melakukan dekripsi
dengan kunci privatnya.
Tentunya
si pihak pertama harus memiliki kunci publik milik pihak kedua untuk melakukan
enkripsi. Pihak pertama bisa mendapatkannya dari pihak yang bersangkutan,
ataupun dari pihak ketiga yang dipercaya.
Teknik
enkripsi asimetris ini jauh lebih lambat ketimbang enkripsi dengan kunci
simetris. Oleh karena itu, biasanya bukanlah pesan itu sendiri yang disandikan
dengan kunci asimetris, namun hanya kunci simetrislah yang disandikan dengan
kunci asimetris. Sedangkan pesannya dikirim setelah disandikan dengan kunci
simetris tadi.
HILL
CIPHER
Hill
Cipher merupakan penerapan aritmatika modulo pada kriptografi. Teknik
kriptografi ini menggunakan sebuah matriks persegi sebagai kunci yang digunakan
untuk melakukan enkripsi dan dekripsi.
Hill
Cipher diciptakan oleh Lester S. Hill pada tahun 1929 [2]. Teknik kriptografi
ini diciptakan dengan maksud untuk dapat menciptakan cipher (kode) yang tidak
dapat dipecahkan menggunakan teknik analisis frekuensi. Hill Cipher tidak
mengganti setiap abjad yang sama pada plaintext dengan abjad lainnya yang sama
pada ciphertext karena menggunakan perkalian matriks pada dasar enkripsi dan
dekripsinya.
Hill
Cipher yang merupakan polyalphabetic cipher dapat dikategorikan sebagai block
cipher [2] karena teks yang akan diproses akan dibagi menjadi blokblok dengan
ukuran tertentu. Setiap karakter dalam satu blok akan saling mempengaruhi
karakter lainnya dalam proses enkripsi dan dekripsinya, sehingga karakter yang
sama tidak dipetakan menjadi karakter yang sama pula.
Hill
Cipher termasuk kepada algoritma kriptografi klasik yang sangat sulit
dipecahkan oleh kriptanalis apabila dilakukan hanya dengan mengetahui berkas
ciphertext saja. Namun, teknik ini dapat dipecahkan dengan cukup mudah apabila
kriptanalis memiliki berkas ciphertext dan potongan berkas plaintext. Teknik
kriptanalisis ini disebut known- plaintext attack [1].
Dasar
Teknik Hill Cipher
Dasar
dari teknik Hill Cipher adalah aritmatika modulo terhadap matriks. Dalam
penerapannya, Hill Cipher menggunakan teknik perkalian matriks dan teknik
invers terhadap matriks. Kunci pada Hill Cipher adalah matriks n x n dengan n
merupakan ukuran blok. Matriks K yang menjadi kunci ini harus merupakan matriks
yang invertible, yaitu memiliki inverse K-1 sehingga :
Kunci
harus memiliki invers karena matriks K-1 tersebut adalah kunci yang digunakan
untuk melakukan dekripsi.
Teknik
Enkripsi pada Hill Cipher
Proses
enkripsi pada Hill Cipher dilakukan per blok plaintext. Ukuran blok tersebut
sama dengan ukuran matriks kunci. Sebelum membagi teks menjadi deretan
blok-blok, plaintext terlebih dahulu dikonversi menjadi angka, masing-masing
sehingga A=1, B=2, hingga Y=25. Z diberi nilai 0.
Tabel : Konversi alfabet ke angka dalam hill cipher
Secara
matematis, proses enkripsi pada Hill Cipher adalah:
C = K . P (2)
C = Ciphertext
K = Kunci
P = Plaintext
Jika terdapat plaintext P:
P = STRIKE NOW
Maka plaintext tersebut dikonversi menjadi:
P = 19 20 18 9 11 5 14 15 23
Plaintext tersebut akan dienkripsi dengan
teknik Hill Cipher, dengan kunci K yang merupakan matriks 2×2.
Karena matriks kunci K berukuran 2, maka
plaintext dibagi menjadi blok yang masing-masing bloknya berukuran 2 karakter.
Karena karakter terakhir tidak ada memiliki pasangan, maka diberi pasangan
karakter yang sama yaitu W. P menjadi STRIKENOWW. Blok pertama dari plaintext P
adalah :
Blok plaintext ini kemudian dienkripsi dengan
kunci K melalui persamaan (2).
Hasil perhitungan menghasilkan angka yang
tidak berkorespondensi dengan huruf-huruf, maka lakukan modulo 26 pada hasil tersebut.
Sehingga, C1,2 menjadi:
Karakter yang berkorespondensi dengan 7 dan
20 adalah G dan T. maka S menjadi G dan T menjadi T. Setelah melakukan enkripsi
semua blok pada plaintext P maka dihasilkan ciphertext C sebagai berikut:
P = STRIKENOW
C = 7 20 14 11 7 11 4 21 19 11
C = GTNKGKDUSK
Dari ciphertext yang dihasilkan terlihat
bahwa Hill Cipher menghasilkan ciphertext yang tidak memiliki pola yang mirip dengan
plaintextnya.
Teknik Dekripsi pada Hill Cipher
Proses dekripsi pada Hill Cipher pada
dasarnya sama dengan proses enkripsinya. Namun matriks kunci harus dibalik
(invers) terlebih dahulu. Secara matematis, proses dekripsi pada Hill Cipher
dapat diturunkan dari persamaan (2).
Menjadi persamaan proses dekripsi:
Dengan menggunakan kunci,
maka proses dekripsi diawali dengan mencari
invers dari matriks K. Mencari invers dapat dilakukan dengan menggunakan metode
operasi baris (row operation) atau metode determinan [3]. Setelah melakukan
perhitungan, didapat matriks K-1 yang merupakan invers dari matriks K, yaitu:
Kunci K-1 yang digunakan untuk melakukan
dekripsi ini telah memenuhi persamaan (1) karena:
Ciphertext C = GTNKGKDUSK, akan didekripsi
dengan menggunakan kunci dekripsi K-1 dengan persamaan (3). Proses dekripsi ini
dilakukan blok per blok seperti pada proses enkripsi. Pertama- tama ubah
huruf-huruf pada ciphertext menjadi urutan numerik.
C = 7 20 14 11 7 11 4 21 19 11
Proses dekripsi dilakukan sebagai berikut:
dan blok kedua:
Setelah semua blok selesai didekripsi, maka
didapatkan hasil plaintext:
P = 19 20 18 9 11 5 14 15 23
P = STRIKENOW
TEKNIK KRIPTANALISIS TERHADAP HILL CIPHER
Kriptanalisis terhadap Hill Cipher sangat
sulit jika dilakukan dengan ciphertext-only attack, terlebih apabila matriks
kunci yang digunakan berukuran besar. Kesulitan ini disebabkan oleh ciphertext
Hill Cipher yang tidak memiliki pola dan setiap karakter dalam satu blok saling
mempengaruhi karakter lainnya.
Teknik yang dapat digunakan untuk melakukan
kriptanalisis terhadap Hill Cipher adalah knownplaintext attack. Jika
kriptanalisis memiliki pecahan plaintext dan ciphertext yang saling
berkorespondensi, maka Hill Cipher dapat dipecahkan. Namun proses yang cukup
sulit adalah untuk menentukan panjang kunci yang digunakan.
Hal ini menjadi salah satu kekuatan yang dimiliki
oleh Hill Cipher. Cara yang dapat dilakukan hanya dengan mencari tahu panjang
kunci atau dengan melakukan perkiraan dan percobaan.
Kemungkinan terburuk yang dimiliki oleh Hill
Cipher adalah ketika seorang kriptanalis memiliki potongan plaintext dan
ciphertext yang berkorespondensi serta mengetahui panjang kunci yang digunakan.
Dengan informasi ini, kriptanalis dapat memecahkan Hill Cipher dengan sangat
mudah. Misalkan kriptanalis mengetahui panjang kunci K adalah 2 dan memiliki
potongan berkas plaintext P dan C sebagai berikut:
P = STRI
C = GTNKGKDUSK
Dari informasi yang dimiliki, maka diketahui
bahwa karakter ST pada plaintext berkorespondensi dengan karakter GT, dan
karakter RI dengan NK. Pemecahan dapat dilakukan dengan persamaan linier
Misalkan kunci direpresentasikan dengan:
Plaintext P dengan:
Ciphertext C dengan:
Dengan menerapkan persamaan (2) maka
persamaan linier yang dapat dibentuk dari contoh adalah:
Dengan menyelesaikan persamaan (i) dan
persamaan (ii) lalu persamaan (iii) dan persamaan (iv) memakai aritmatika
modulo 26, maka nilai a, b, c, dan d didapat:
a = 5
b = 6
c = 2
d = 3
Dengan nilai a, b, c, dan d maka kunci K
didapatkan, yaitu:
Dengan kunci K tersebut, kriptanalis hanya
perlu melakukan dekripsi terhadap ciphertext keseluruhan untuk mendapatkan
plaintext seutuhnya.
















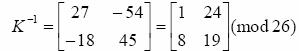

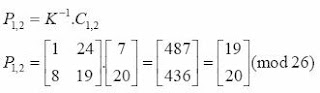


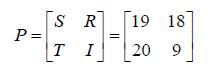



Tidak ada komentar:
Posting Komentar